Una cicloide es una curva generada por un punto perteneciente a una circunferencia generatriz al rodar sobre una línea recta directriz, sin deslizarse.
Te invito a mirar este video que nos da información sobre la generación de la cicloide.
Si prestas atención al movimiento que realiza el pié de una persona que está corriendo a velocidad constante, verás que la trayectoria que describe es exactamente una cicloide.
(Te invito a que leas el párrafo correspondiente a “Andar y Correr” de "Física Recreativa I" de Jacob Perelman)
Es muy interesante su construcción que está relacionada con los óvalos de Cassini .
Si quieres realizarla usando sólo compás y escuadra también es posible y así lograrás una "cinta colgante" con tu propio diseño.
La Lemniscata
Una lemniscata
es el lugar geométrico de los puntos del plano tales que el producto de sus
distancias a dos puntos fijos llamados focos es constante.
Su definición es muy similar a la definición de la elipse.
Fue en el año 1694 cuando
Jakob Bernoulli describió esta curva y la llamó lemniscus, que en Latín
significa "cinta colgante"Es muy interesante su construcción que está relacionada con los óvalos de Cassini .
Si quieres realizarla usando sólo compás y escuadra también es posible y así lograrás una "cinta colgante" con tu propio diseño.
Y,
de forma aproximada, también está presente en la naturaleza. El analema, que es
la curva descrita por la posición del Sol observada todos los días del año a la
misma hora y desde la misma posición, se asemeja a una lemniscata:
César nos mandó esta imágen de un analema fotografiado en España.
Es una belleza!
La Cuadratriz
La Cardioide
El conjuntode Mandelbrot contiene un número infinito de copias ligeramente distorsionadas
de sí mismo y el bulbo central de cualquiera de estas copias más pequeñas es
aproximadamente una cardioide.
A Moni M. le encanta esta curva:
La “bruja” de Agnesi es el lugar geométrico de los puntos P que se generan por la intersección de las rectas horizontales y = A, y las rectas verticales x= B cuando el punto A recorre la circunferencia.
La Revista “En
Blanco & Negro” propone una situación interesante para trabajar con
esta curva.
Particularidades:
César nos mandó esta imágen de un analema fotografiado en España.
Es una belleza!
La
cuadratriz
es una curva descubierta por los antiguos matemáticos griegos que resuelve
dos de los problemas famosos de la época: la trisección del ángulo y la
cuadratura del círculo. No se sabe quienes descubrieron sus propiedades, pero se
las asocian con Dinostrato, Nicomedes e Hipias.
Se
puede construir de la siguiente forma:
El
segmento de recta ab se mueve
uniformemente desde la posición indicada hacia abajo hasta coincidir con oc. Al mismo tiempo, el segmento ao rota uniformemente en el sentido de
las agujas del reloj a partir del punto o
desde la posición oa hasta coincidir
con oc, en el mismo tiempo que ab tarda en llegar a oc. La curva trazada por la intersección
de los dos segmentos a medida que se mueven es la cuadratriz de Hipias.
Te invito a que mires este video
sobre la cuadratriz de Hipias. Esta muy interesante!
La cuadratriz de Hipias no es la única curva mecánica
que permite cuadrar un círculo.
La forma de esta bellísima curva es la de un
“corazoncito”
Este video te ayudará a construir
la cardioide
usando geogebra
Pero esta curva también aparece
en la naturaleza, ¿dónde? EN LAS SEMILLAS como por ejemplo la semilla de Lotus japonicus
La
catacáustica de una curva es la envolvente de los rayos reflejados por dicha
curva, a partir de un haz de rayos procedentes de un punto dado (que puede ser
el infinito).
La catacáustica de un círculo con respecto a un punto de la
circunferencia es una cardioide. La podemos ver cuando
tomamos una taza de café.
Simplemente DELICIOSO!
En el plano complejo, la imagen de
cualquier círculo a través del origen es una cardioide.
Una aplicación
de este resultado es el conjunto de Mandelbrot.
Este conjunto es
uno de los fractales más estudiados. Una propiedad fundamental de los fractales es la autosimilitud o autosemejanza, que se refiere a una
cierta invariabilidad con relación a la escala, o dicho de otro modo, al
acercarse a ciertas partes de la imagen reaparece en miniatura la imagen total.
Un mismo motivo aparece a distintas escalas, a un número infinito de escalas.
A Moni M. le encanta esta curva:
La “Bruja” de Agnesi
La “bruja” de Agnesi es una curva que
Fermat había estudiado en 1703, y para la que Grandi en 1718 había dado un
método de construcción.
Lo de “bruja” fue un error de traducción. Grandi llamó a la curva versoria en latín, y vertiera en italiano. Es un término naval, que
identifica la cuerda o cabo que hace girar la vela. María Gaetana Agnesi
escribió a su vez la versiera,
añadiendo el artículo femenino. John
Colson, un traductor de Cambridge con poco conocimiento del italiano, llama a la curva witch (“bruja”), debido a que “confundió” vertiera con avversiera (que en
italiano significa diablesa o bruja).
Para definir la curva se considera la circunferencia de radio
a y centro (0,a). Sea OT = 2a un diámetro
de dicha circunferencia. Si A es un punto de la circunferencia, la recta que
pasa por (0,0) y A, intersecta a la recta tangente a la circunferencia por T, (y=2 a)
en el punto B. La perpendicular a y =
0 por B y la horizontal por A, determinan el punto P.
La “bruja” de Agnesi es el lugar geométrico de los puntos P que se generan por la intersección de las rectas horizontales y = A, y las rectas verticales x= B cuando el punto A recorre la circunferencia.
Te invito a que mires este video
sobre la “bruja”de Agnesi
Algunas particularidades de la “bruja”
ÄEs
una función par (simétrica respecto al eje de ordenadas)
ÄEs
creciente si x <0 y decreciente si x >0
ÄTiene
un máximo en el punto (0,1
ÄEl
eje de abscisas es una asíntota horizontal
ÄEl área entre la curva y el eje de abscisas es Pi!...(sólo hay que hallar la integral de la función)
¡Otro hechizo de la curva, un contorno infinito encierra un
área finita!
Y la
belleza de los cuerpos de Iratxe Ansa y Nicolás Maire nos hechizan con su
coreografía de Ofrenda de Sombras.(La bruja de Agnesi aparece en la curvatura
del cuerpo de Iratxe)
Fotografía tomada de “El Libro de las Curvas” de Pablo y
Alfonso Olalquiaga. Fundación ESTEYCO (pág. 142)
En Estadística,
la Distribución de Cauchy de una variable aleatoria, se expresa por
una “Bruja” de
Agnesi.
El Folio de Descartes
Es una curva de tercer grado, con
dos ramas infinitas
que tienen una asíntota común y se cortan formando un lazo
sencillo, semejante a una hoja ovadolanceolada.
Esta curva fue estudiada
inicialmente por Descartes y Roberval en 1638 (a través de un intercambio de
correspondencia con Mersenne) y más tarde por Huygens en 1672. En sus
estudios, Descartes y Roberval determinaron correctamente el trazado de la
curva en el primer cuadrante. Sin embargo, se cree que (erróneamente) este
formato de hoja se repite en los otros tres cuadrantes por lo que se le dio el
nombre de flor de jazmín.
El método de determinación de la
tangente a la curva fue propuesto por Roberval y su naturaleza asintótica por
Huygens en 1692.
Esta curva es también conocida
por el nombre francés
de nœud Ruban.
Ø
El área del bucle y el área comprendida entre
las ramas infinitas de la curva y su asíntota son iguales y valen (l/3)2.
Ø
La amplitud máxima del bucle vale
aproximadamente 0,448 l
y la distancia DO es igual a l.(3)1/2/3.
Para realizar su construcción:
Se considera un punto A de coordenadas (a, a) y las dos
parábolas P y Q de vértice O que pasando por este punto tienen el origen como
vértice y respectivamente Ox y Oy como ejes de simetría.
Se traza un vector cualquiera que se cruce con las dos
parábolas en los puntos B y C. La combinación armónica M de O en relación a B y
C describe un Folio de Descartes.
La Concoide de Nicomedes
La concoide,
en general, es la curva que en su prolongación se aproxima constantemente a una
recta (la directriz) sin tocarla nunca; la
directriz es recíprocamente la asíntota de la concoide.
La
concoide
de Nicomedes es el lugar geométrico de los puntos M para los
cuales:
OM=OP+l u OM=OP-l
Siendo O el polo
de la concoide
Se distinguen
tres casos:
a>l a=l a<l
El nombre de concoide se debe a su parecido con las conchas que
tanto abundaban en las playas griegas. Aunque su creador es Nicomedes,
un geómetra griego (280
– 210 a .
de C.), que la investigó junto a otras 16 curvas matemáticas, esta curva fue atribuida a Pappus.
Nicomedes quiso utilizar la concoide para resolver los problemas de la duplicación del cubo
y de la trisección del ángulo y
de hecho la curva sirve para trisecar cualquier ángulo.
Para construir una concoide
de Nicomedes en el caso en el que a<h,
se trazan desde el punto O hasta la
recta n un conjunto de segmentos O1, O2, O3, O4,
…prolongando en los dos sentidos estos segmentos con longitud igual a AB a
partir de los puntos 1, 2, 3, …se obtienen los puntos que definen la curva
Para el caso en el que a=h se procede de la misma
manera pero se observa que desaparece el lazo
Lo mismo ocurre cuando a>h
Si quieres ver cómo se modifica la curva ingresa aquí
CURIOSIDAD:
Existe este dispositivo que permite generar la concoide
por el método de Suardi
El perno M, fijado a s (directriz),
recorre la ranura rectilínea, practicada en el plano en el que se apoya el
mecanismo. Durante su movimiento, la s es forzada a pasar al pivote O, fijado de tal manera que su distancia
desde la ranura (fijada en el plano) sea OH
= a. Dos puntos se colocan en P y Q,
con MP = MQ = b; estos puntos describen las dos ramas de la concoide teniendo como base la línea
recta de la ranura y el intervalo b.
El mecanismo permite variar de forma continua los parámetros a y b
que determinan la forma de la concoide, y es por lo tanto flexible. En el
caso particular de la concoide de Nicomedes, los parámetros tienen
valores prefijados.
La Curva de Lamé
Esta curva fue estudiada por
Gabriel Lamé en 1818, es también llamada superelipse.
Vulgarmente se podría decir que
es la combinación de una elipse y un rectángulo.
Es la generalización de una
elipse y su ecuación es :
Algunos casos particulares para
diferentes valores de n
Para construirla puedes ingresar aquí
Piet Hein hizo un uso
arquitectónico de esta curva.
También es conocida
como epicicloide de Huygens.
La nefroide es la curva descripta por un punto de una circunferencia que, sin
deslizarse, rueda alrededor de otra circunferencia en el caso en que la
relación entre los radios de ambas es de ½.
También es la envolvente de las
cuerdas de un círculo cuando los extremos de la cuerda recorren la
circunferencia en el mismo sentido y uno a triple velocidad que el otro.
Aquí tienes una nefroide en movimiento
Una situación común donde se pueden observar catacáusticas
en cuando la luz brilla a través de un vaso de bebida. El vaso proyecta una
sombra, pero también produce una región curva de luz brillante.
Catacáustica en forma de nefroide en el fondo de una taza de té.
Aquí se
observa una colonia de zooides independientes (Clavelina Lepadiformes), muy próximos entre sí, unidos por
estolones rastreros. Si miramos la “forma” de cada uno, es la de una nefroide. La forma de este
empaquetamiento compacto es similar al de una piña de piñones o a una mazorca
de maíz.
Hasta
hace poco se creía que el empaquetamiento más compacto se conseguía mediante un
poliedro de 14 caras, propuesto en 1887 por Lord Kelvin, pero recientemente, en
1993, Dennis Weaire y R. Phelan han propuesto una estructura celular cuya área
es un 0,3% inferior a la del poliedro de Kelvin. La estructura está formada por
ocho celdas, seis con 14 caras y dos con 12.
Aquí
podrán ver una superficie plana construída sobre una nefroide .....
y aquí el
“riñón” generado por la rotación de una nefroide
La Clotoide
Aquí se observa el diseño de la
plaza de Sergel en Estocolmo, Suecia para el que utiliza n=5/2 y con a=6 y b=5.
En cambio para su mesa diseñada
en 1968 utiliza a=3 y b=2 para el mismo valor de n.
Estos diseños
corresponden a la generalización de la superelipse cuando a=b=1 y se considera la desigualdad <1
La Nefroide
Fue estudiada por Huygens en su Tratado de la luz (1690) como solución del
problema de determinación de la envolvente de los rayos reflejados por un círculo
a partir de un haz de rayos paralelos.
Por Jacques Bernoulli en 1692, por Daniel Bernoulli en 1725
y por Proctor, en 1878 que le dio ese nombre a una epicicloide de dos cúspides (por su parecido a la forma de un riñón).
También es conocida
como epicicloide de Huygens.
La nefroide es la curva descripta por un punto de una circunferencia que, sin
deslizarse, rueda alrededor de otra circunferencia en el caso en que la
relación entre los radios de ambas es de ½.
La nefroide también es la
envolvente de los diámetros de una circunferencia que rueda alrededor de otra
de igual radio.
También es la envolvente de las
cuerdas de un círculo cuando los extremos de la cuerda recorren la
circunferencia en el mismo sentido y uno a triple velocidad que el otro.
La evoluta de la nefroide sigue siendo….. una nefroide !
Aquí tienes una nefroide en movimiento
Aquí puedes construir un ciclo completo colocando los valores 20,40 20
Una situación común donde se pueden observar catacáusticas
en cuando la luz brilla a través de un vaso de bebida. El vaso proyecta una
sombra, pero también produce una región curva de luz brillante.
Para el
punto radiante en el infinito la catacáustica es la nefroide
Catacáustica en forma de nefroide en el fondo de una taza de té.
La naturaleza también nos muestra nefroides
Aquí se
observa una colonia de zooides independientes (Clavelina Lepadiformes), muy próximos entre sí, unidos por
estolones rastreros. Si miramos la “forma” de cada uno, es la de una nefroide. La forma de este
empaquetamiento compacto es similar al de una piña de piñones o a una mazorca
de maíz.
Hasta
hace poco se creía que el empaquetamiento más compacto se conseguía mediante un
poliedro de 14 caras, propuesto en 1887 por Lord Kelvin, pero recientemente, en
1993, Dennis Weaire y R. Phelan han propuesto una estructura celular cuya área
es un 0,3% inferior a la del poliedro de Kelvin. La estructura está formada por
ocho celdas, seis con 14 caras y dos con 12.
Aquí
podrán ver una superficie plana construída sobre una nefroide .....
y aquí el
“riñón” generado por la rotación de una nefroide
La clotoide, también denominada espiral de Cornú en
honor de Marie Alfred Cornu, espiral de Euler o espiral de Fresnel, es una
curva cuyo radio de curvatura r varía gradualmente de manera
inversamente proporcional a la distancia
s recorrida sobre la curva
La expresión matemática usual de la clotoide es:
r(s)·s = C
siendo:
ρ: el radio de curvatura
s: la distancia o arco recorrido sobre la curva
C: la constante de la clotoide
La clotoide
tiene la propiedad de que su curvatura en cualquier punto es proporcional a la distancia
a lo largo de la curva medida desde el origen. Esta propiedad hace que sea útil
como curva de transición (ver pág 11-11) en el trazado de autopistas o vías de ferrocarril, puesto
que un vehículo que siga dicha curva a velocidad constante tendrá una
aceleración angular variable proporcionalmente con la distancia recorrida, y se
evitarán discontinuidades en la aceleración centrífuga de los vehículos.
(Mirar primeros 2,43 min)
Se utiliza como curva de
transición entre un tramo recto y otro circular. De esta manera el tipo de curva
más usual en carreteras es:
"Tramo recto - Clotoide- Circular - Clotoide - Tramo
recto".
Igualmente las secciones de la clotoide son usadas comúnmente en montañas rusas por lo que algunas
vueltas completas se conocen como loops "clotoides".
Permiten una variación gradual
del radio de curvatura de la trayectoria con el propósito de suavizar el
encuentro de una recta con una curva circular de un radio determinado.
La fuerza centrifuga es nula en
una recta. Al entrar en una curva adquiere un valor determinado lo cual hace
que un vehículo corra el riesgo de salirse a la entrada de una curva si no
reduce la velocidad, con lo cual disminuirá el valor de la fuerza centrifuga.
Una curva de transición al tener una variación gradual, uniforme de su radio,
la fuerza centrífuga también varía de una forma gradual, uniforme. Así se
pueden evitar los accidentes debidos a variaciones bruscas en el radio de curvatura
y consecuentemente en la fuerza centrífuga.
Ventajas:
Ø
Permiten una marcha
regular y cómoda, la adaptación al paisaje es excelente, reduce los movimientos
de tierra con respecto a un trazado clásico de rectas y círculos y de este modo
su impacto ambiental es menor.
Ø
Mejora la perspectiva
desde el punto de vista del conductor. Las curvas de transición permiten una
visión a mayor distancia y le dan al conductor la sensación de un camino
perfectamente regulado.
Los tipos de curvas de
transición más utilizadas son: La clotoide, la lemniscata
y la parábola cúbica.
“Los trazados de
carreteras, con adecuados peraltes y clotoides, mantienen la variación de la
aceleración transversal, por debajo de los o,5 m/seg2 , para
velocidades de circulación superiores a 80 km/h . Existen otros condicionantes que
suelen establecerse en las “Normas de trazado” que aseguran una conducción
segura y confortable. La carretera, bien trazada, debe guiar al coche con muy
escaso esfuerzo, físico e intelectual, del conductor, para quien la clotoide,
sin él muchas veces saberlo, forma parte de su vida porque probablemente se la
haya salvado en alguna ocasión.”
Información y
fotografía tomadas de “El Libro de las Curvas” de
Pablo y Alfonso Olalquiaga. Fundación ESTEYCO. Pág 46
Para saber más ingresa aquí.
O tal vez quieras recorrer a 70 km/h los dieciséis
“rulos” de Half Pipe en Elitch Gardens, Denver- Colorado, donde se lucen las clotoides.
“Pero sea lo que fuere, no cabe duda de que
la expresión de un fenómeno resistente, intrínseca y aparentemente imposible,
es algo siempre antiestético para el observador que así lo comprende”
Eduardo Torroja. “Razón y ser de los
tipos estructurales”
“Qué duras se hacen las curvas. Cuando son muchas. Y muy
curvas. ¿Quién dice que el arte es curvo? ¡Qué geometría desquiciada! Y esa
estructura que sufre la locura o el arte, ¿acaso se acuerda nadie de ella?,
¿acaso nadie se apiada? Qué cosas, qué cosas…La Verdad , de suyo detesta lo
curvo.¿Y la ingeniería? Quién sabe, quien sabe…
Tomado de “El Libro de las Curvas” de Pablo y Alfonso
Olalquiaga. Fundación ESTEYCO. Pág 165
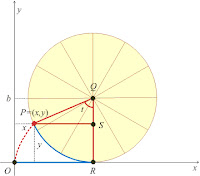
La catenaria
es la curva que forma un hilo (o cadena) homogéneo e inextensible suspendido de
dos puntos (sus extremos), debido a su propio peso.
Galileo no encontró la solución
a este problema clásico cuando creyó que la curva formada por la cadena era un
arco de parábola. Hacia 1690 Leibnitz, Huygens y Jean Bernoulli establecieron
la correcta formulación de la curva.
Siendo a la distancia al vértice de la curva desde el origen de
coordenadas.
Particularidades:
Ä La catenaria
tiene por evolución a otra curva célebre, la tractriz que es a su vez
envolvente de la catenaria.
Ä La sección transversal de las velas
infladas por el viento es igualmente una catenaria, porque la fuerza horizontal
que el viento ejerce sobre la vela es análoga a la acción de la fuerza de la
gravedad sobre la cadena. En este caso, la curva también se denomina velaria.
Ä Si hacemos rodar una parábola a lo
largo de una recta, el foco de la parábola describe una catenaria. Cerca del vértice, la parábola y la catenaria son casi coincidentes.
Ä La longitud de un arco de la catenaria
medida a partir de su sima (x=0) vale
s=a.Shx/a.
La relación de la longitud del
arco, s, y su ordenada y, es: s2+ a2=y2
Ä El área del rectángulo mixtilíneo entre
la curva, el eje de abscisas, el eje de ordenadas y la vertical al punto de la
curva considerado, tiene por valor S.a
Ä La catenaria es
el antifunicular de carga de un arco de sección constante, que no estará
sometido sino a esfuerzos de compresión cuando adopte esta geometría.
La catenaria
invertida (arco) es un elemento arquitectónico empleado, entre otros, por
Antonio Gaudi.
También puedes admirar un arco de catenaria en el bellísimo “Jefferson Memorial” en Saint Louis, Missouri
EE.UU.
Y aquí podrás reproducirlo para hacer algunos cálculos.
Si quieres obtener una catenaria a partir de un conjunto de
bolitas suspendidas prueba aquí.
¿Es lo mismo una parábola que una catenaria?
La catenaria y la parábola son diferentes si están formadas por materiales pesados:
en la catenaria la distribución del peso de la cadena es uniforme
para cada longitud de arco; en los puntos suspendidos, sin embargo, donde de la
cadena cuelgan los tirantes que sujetan el plano de un puente, la distribución
del peso es uniforme por unidad horizontal de longitud y la curva descripta es
una parábola.
En los grandes puentes
colgantes, donde el peso de las cadenas es del mismo orden de dimensión del
plano de la carretera, la curva resultante está entre una parábola y una catenaria. En la figura se ve la curva catenaria,
descripta por una cadena suspendida, superpuesta a la parábola resultante
cuando a la cadena se le cuelgan los tirantes que sostienen el plano horizontal
del puente.
Como cierre, cuando vamos a la
gala en un teatro de Opera, tenemos una bellísima catenaria
para clausurar sus escalinatas…
La Serpentina
Esta curva fue estudiada por Newton en 1701.
Su definición se
encuentra en su libro llamado "Lexicon Technicum" publicado en
Londres en 1710. Él fue el primero en emprender un estudio sistemático de las
ecuaciones cúbicas. Las clasificó en 72 casos distintos, pero faltaban 6 en su
clasificación. También fue estudiada por L'Hôpital y Huygens
Para definir la curva se parte de una circunferencia de
radio r. Por el extremo A del diámetro AB
de la circunferencia de radio r se traza una recta
secante que corta a la circunferencia en el punto C y a una recta
paralela al diámetro a una distancia d, en un punto D. Por el
punto C se traza una paralela
al diámetro y la perpendicular a ésta por el punto D, la intersección de ambas determina
el punto P.
El lugar geométrico descripto por el punto P al girar la recta AC alrededor
del punto A es una curva denominada serpentina de Newton.
La ecuación cartesiana
de la curva es:
x2.y +
a.b.y – a2.x =0 ; a.b>0
y la ecuación
explícita es:
La clasificación de Newton de las cúbicas fue criticada por
Euler. Plücker más tarde hizo una clasificación más detallada de las cúbicas
con 219 casos.
La Cisoide
de Dioclés
En el siglo VI a.c. Dioclés la concibió para solucionar el
problema de la duplicación del cubo, que junto con el de la cuadratura del
círculo y el de la trisección de un ángulo, fueron los tres grandes problemas
geométricos que reclamaron la atención de los sabios griegos. En el siglo XVII
matemáticos renacentistas como Roberval y Slusse analizaron y profundizaron la definición y el conocimiento de la esta
curva nacida 2000 años antes.
Particularidades:
Ø
La curva es simétrica respecto del eje
horizontal.
Ø
Posee una asíntota vertical para x=a.
Ø
El punto de retroceso para x=0 con radio de
curvatura nula.
Ø
El área comprendida entre la cisoide
y la asíntota es tres veces la del círculo generador.
Ø
El
volumen engendrado por la cisoide girando alrededor de su eje de simetría es
infinito.
Ø
El volumen engendrado por la cisoide girando
alrededor de la asíntota es el doble del volumen engendrado por el círculo
generador girando alrededor del mismo eje.
Ø
El centro
de gravedad se sitúa en relación con la asíntota a 1/5 del diámetro del círculo
generador.
Construcción:
Sea Ay´ la tangente en A al círculo de
diámetro OA=a,
Se traza un vector ONP que corte al círculo en N
y Ay´en P.
Al llevar OM=NP, el punto M describe una cisoide
recta.
La cisoide es el lugar geométrico de todos los puntos
M originados al variar el ángulo AoP.
Dioclés construyó la curva limitándose a los puntos
interiores al círculo. Completando este arco de la curva con la
semicircunferencia, se obtiene una forma parecida a una hoja de hiedra, de
donde le viene el nombre de cisoide.
La ecuación de la curva en coordenadas rectangulares es:
Y en coordenadas polares:
a es el diámetro del círculo generador.
Si quieres saber más sobre esta curva ingresa aquí y busca la página 63.
La Estrofoide
de Newton
La estrofoide de Newton, es una hermosa curva algebraica plana de 3º grado, circular y con un
nodo. Citada por Barrow, descripta por Torriccelli
y definida por
Personne de Roverbal (leer pág. 13)hacia 1645, que la
denominó inicialmente ptéroïde (del griego “pteron” que significa ala)
antes de ser rebautizada hacia 1846, por Montucci, quien le
puso el nombre de estrofoide = correa enrollada.
La estrofoide es el lugar geométrico de los puntos M1 y M2. (que
yacen en rayos arbitrarios que pasan por el punto A), para los cuales PM1=PM2=OP (P es un punto
arbitrario del eje Oy).
PARTICULARIDADES:
Ø
Las tangentes en las dos ramas de la curva en O
son ortogonales.
Ø
El volumen encerrado por el bucle girado
alrededor del eje OX es aproximadamente a3/6.
Ø
El matemático inglés T.J. Freeth, en el siglo
XIX, propuso una estrofoide (leer pág 157)evolucionada que facilitaba la construcción de polígonos regulares de 7, 9 y 11 lados.
Ø
Su ecuación en coordenadas polares es p=4.a.cos2t.sen2t.
Ø
Entre la
familia de curvas que resulta se
encuentra la estrofoide
de tres pétalos.
CONSTRUCCIÓN:
Dada una circunferencia de radio a se toman como
ejes su diámetro y la tangente a la circunferencia en el extremo O de
ese diámetro OA; por el punto O se trazan rectas OB que
cortan a la circunferencia en puntos I; llevamos IM=IB; el lugar
del punto M, siendo B el punto en que OB corta a la
tangente a la circunferencia por el punto A define esta curva.
Preciosa imagen
de la curva en la naturaleza aunque la lagartija debería haber dejado su cola
apuntando hacia arriba.
Foto de un
detalle de la fuente de la Cité des Sciences de Paris con la Géode al fondo. La fuente completa es una curva
más complicada.









.bmp)
.bmp)

.bmp)
.bmp)
.bmp)


.bmp)
.bmp)
.bmp)


.bmp)

.bmp)


.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)


.bmp)


.bmp)
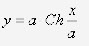
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)



.bmp)
.bmp)

.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
Felicitaciones por el trabajo realizado en este blog.
ResponderEliminarExcelente trabajo, felicitaciones
ResponderEliminarexelente trabajo. Gracias!!
ResponderEliminarExcelente recopilación de curvas y buenos ejemplos.
ResponderEliminarSi me permites, tan solo debo hacerte un humilde comentario. Antoni Gaudí, brillante arquitecto catalán que utilizó la catenaria y otras curvas matemáticas en sus construcciones, fue detenido por responder en catalán a la policía del régimen fascista de Primo de Rivera. Creo que sería un buen homenaje y un signo de respeto mantener en este blog su nombre tal y como el se hacía llamar: Antoni.